Jedes Dreieck ist gleichseitig

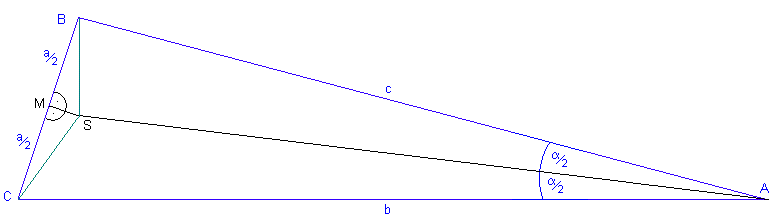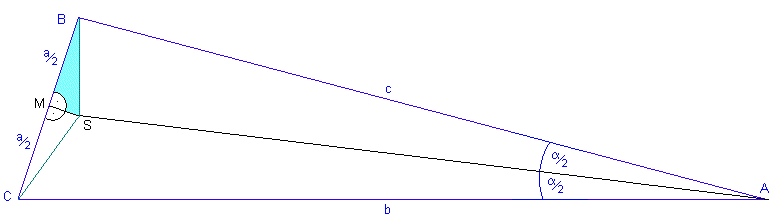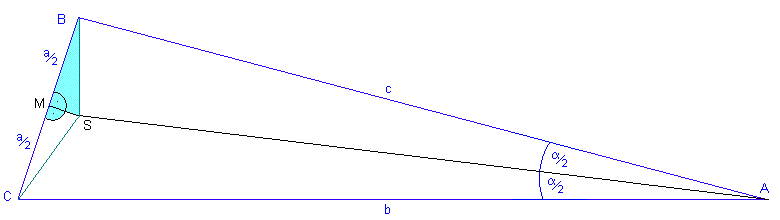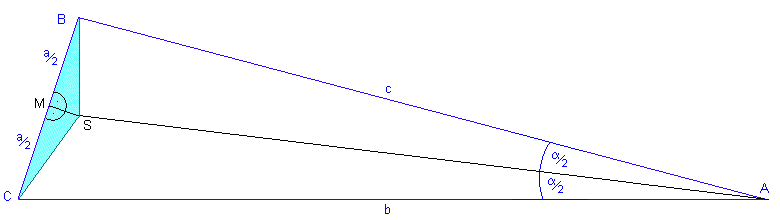
Das ist eine kühne Aussage, aber man kann sie beweisen! Bei dieser Beweisführung wollen wir in zwei Schritten vorgehen: Zunächst zeigen wir, dass jedes Dreieck gleichschenklig ist, und leiten daraus dann die Gleichseitigkeit ab.

Beweisschritt 1: Jedes Dreieck ist gleichschenklig

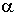Wir beginnen mit einem beliebigen Dreieck, geben die Eckpunkte mit den Großbuchstaben A, B, C, die jeweils gegenüberliegenden Seiten mit den Kleinbuchstaben a, b, c und den Innenwinkel an.

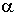Nun zeichnen wir die Winkelhalbierende von und die Mittelsenkrechte auf die gegenüberliegende Seite a ein. Diese beiden Linien treffen sich in ihrem Schnittpunkt S.

Wir ziehen die Verbindungslinien vom Schnittpunkt S zu den Eckpunkten B und C, und betrachten die dadurch entstandenen, grün eingefärbten Teildreiecke BMS und CMS. (weiter >>)