Jedes Dreieck ist gleichseitig

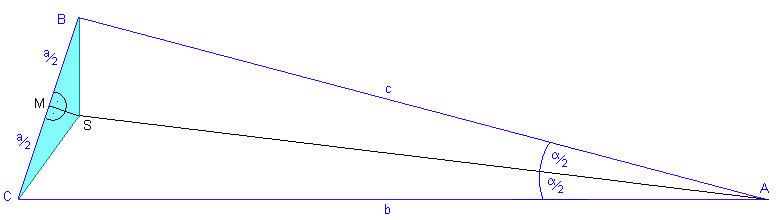
Das ist eine kühne Aussage, aber man kann sie beweisen! Bei dieser Beweisführung wollen wir in zwei Schritten vorgehen: Zunächst zeigen wir, dass jedes Dreieck gleichschenklig ist, und leiten daraus dann die Gleichseitigkeit ab.

Beweisschritt 1: Jedes Dreieck ist gleichschenklig

Wir beginnen mit einem beliebigen Dreieck, geben die Eckpunkte mit den Großbuchstaben A, B, C, die jeweils gegenüberliegenden Seiten mit den Kleinbuchstaben a, b, c und den Innenwinkel an.

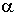Nun zeichnen wir die Winkelhalbierende von und die Mittelsenkrechte auf die gegenüberliegende Seite a ein. Diese beiden Linien treffen sich in ihrem Schnittpunkt S.

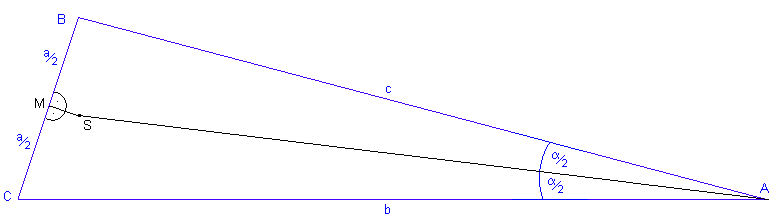
Wir ziehen die Verbindungslinien vom Schnittpunkt S zu den Eckpunkten B und C, und betrachten die dadurch entstandenen, grün eingefärbten Teildreiecke BMS und CMS. Diese beiden Teildreiecke sind kongruent (deckungsgleich), denn sie haben die gemeinsame Mittelsenkrechte, die gleichlangen Seiten und den dazwischenliegenden rechten Winkel. Mit anderen Worten: Das eine Teildreieck kann durch Spiegelung an der Mittelsenkrechten in das andere überführt werden. (weiter >>)