Jedes Dreieck ist gleichseitig

Das ist eine kühne Aussage, aber man kann sie beweisen! Bei dieser Beweisführung wollen wir in zwei Schritten vorgehen: Zunächst zeigen wir, dass jedes Dreieck gleichschenklig ist, und leiten daraus dann die Gleichseitigkeit ab.

Beweisschritt 1: Jedes Dreieck ist gleichschenklig

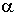Wir beginnen mit einem beliebigen Dreieck, geben die Eckpunkte mit den Großbuchstaben A, B, C, die jeweils gegenüberliegenden Seiten mit den Kleinbuchstaben a, b, c und den Innenwinkel an.

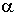Nun zeichnen wir die Winkelhalbierende von und die Mittelsenkrechte auf die gegenüberliegende Seite a ein. Diese beiden Linien treffen sich in ihrem Schnittpunkt S.

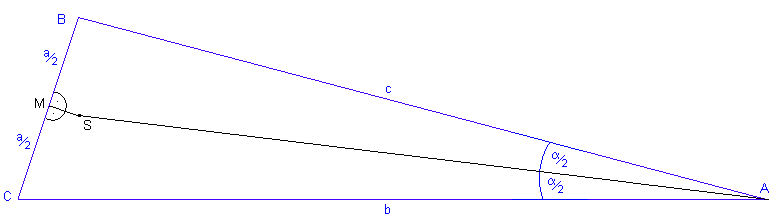
Wir ziehen die Verbindungslinien vom Schnittpunkt S zu den Eckpunkten B und C, und betrachten die dadurch entstandenen, grün eingefärbten Teildreiecke BMS und CMS. Diese beiden Teildreiecke sind kongruent (deckungsgleich), denn sie haben die gemeinsame Mittelsenkrechte, die gleichlangen Seiten und den dazwischenliegenden rechten Winkel. Mit anderen Worten: Das eine Teildreieck kann durch Spiegelung an der Mittelsenkrechten in das andere überführt werden. Aus dieser Kongruenz folgt, dass auch die Seiten BS und CS gleichlang sind.

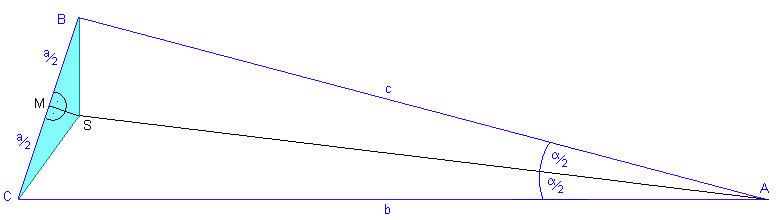
Jetzt ziehen wir vom Punkt S aus jeweils eine senkrechte Linie auf die Seiten b und c, und benennen die Schnittpunkte mit X und Y. Wir betrachten die dadurch entstandenen, lila eingefärbten Teildreiecke ASX und ASY. Diese beiden Teildreiecke sind ebenfalls kongruent, denn sie haben als gemeinsame Seite die Winkelhalbierende von 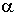und die daran anliegenden, jeweils gleichgroßen Winkel 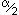und 90°, oder anders beschrieben: Ein Teildreieck geht durch die Spiegelung an der Winkelhalbierenden in das andere über. Aus dieser Kongruenz folgt, dass auch die Seiten SX und SY sowie AX und AY jeweils gleichlang sind.

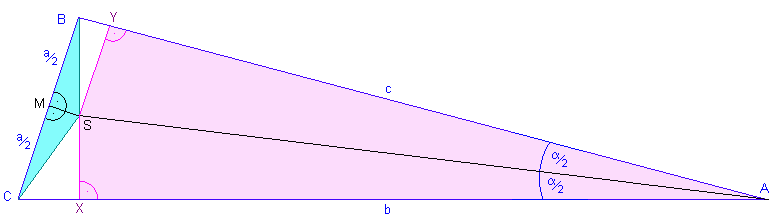
Schauen wir uns die noch übriggebliebenden, hier gelb eingefärbten Teildreiecke BSY und CSX an: Auch wenn es in dieser Zeichnung nicht so aussieht, sind auch diese beiden Teildreiecke kongruent! Beides sind nämlich rechtwinklige Dreiecke mit jeweils gleichlangen Katheten SX und SY, wie wir kurz zuvor gesehen haben, und ebenfalls gleichlangen Hypotenusen BS und CS, wie wir weiter oben bereits erkannt haben. Daraus folgt zwangsläufig, dass auch die Seiten BY und CX gleichlang sind.

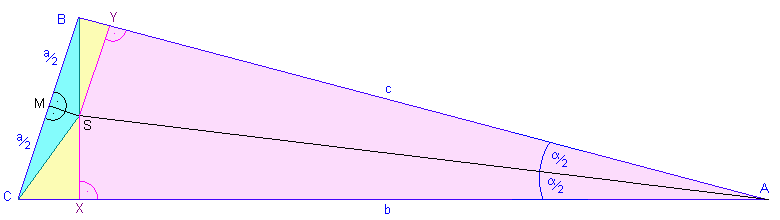
Da sowohl BY und CX als auch AY und AX (siehe oben) jeweils gleichlang sind, müssen auch die addierten Strecken AY + BY und AX + CX, d.h. AB und AC die gleiche Länge haben. Diese sind aber nichts als die Seiten c und b des Gesamt-Dreiecks, die also gleichlang sind. Wir haben damit bewiesen, dass ein beliebiges Dreieck gleichschenklig ist! (weiter >>)